쩡으니
쩡으니

[프로그래머스] 섬 연결하기 - 42861 (Java)

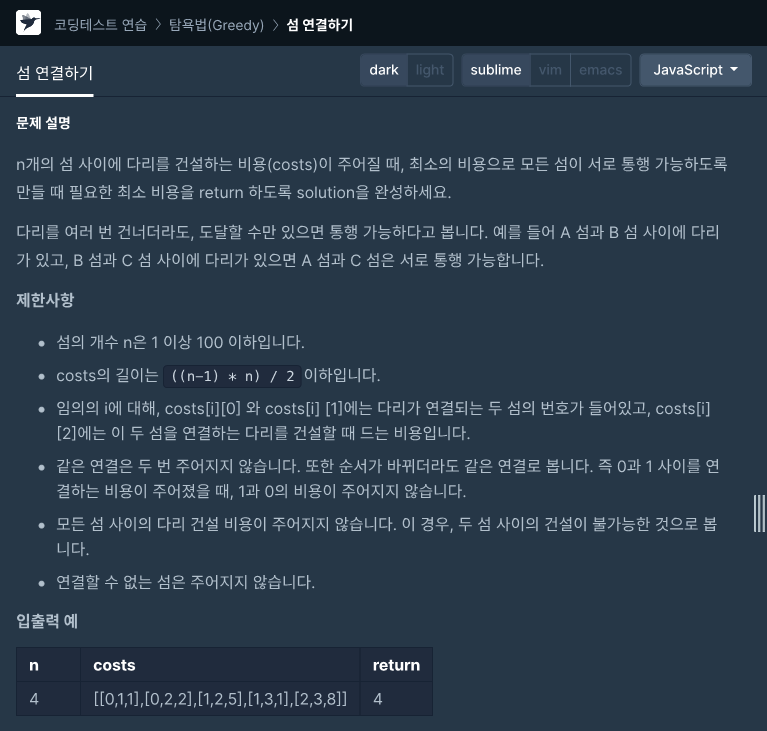
섬 연결하기

이번 문제는 크루스칼을 이용하여 푸는 방법이다.

Union find

우선 크루스칼을 알기 전에 유니온 파인드 알고리즘 부터 알아가야 한다.

유니온 파인드란 여러개의 노드가 존재할 때 연결된 노드들을 같은 집합 구성원으로 묶어주는 알고리즘이다.

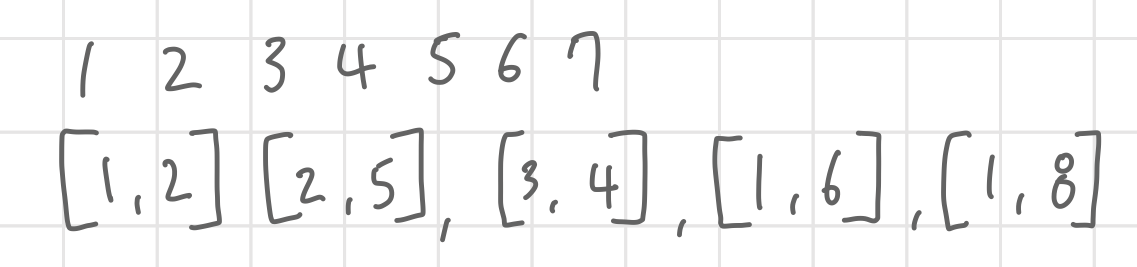
섬 연결하기

그림과 같이 각 노드들 번호와 연결된 노드들이 주어졌을 때, 몇개의 집합이 있는 지, 각 노드들은 어떤 노드들과 같은 집합에 있는지를 판단할때 유용하게 사용된다.

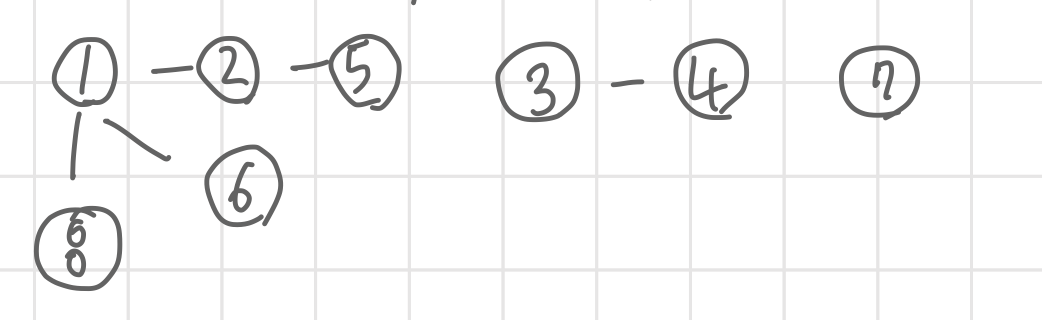
섬 연결하기

그림 처럼 입력값으로 그림을 그려보면 5번과 6번이 같은 집합인지 확인할려면 2번을 갔다가 1번을 갔다가 6번을 가야하는 귀찮은 과정이 있다.

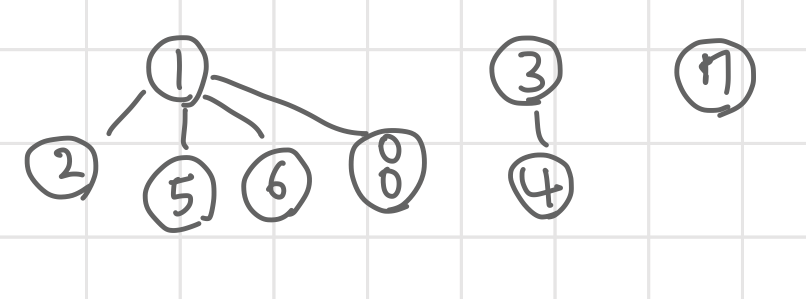
섬 연결하기

유니온 파인드를 한 결과이다. 각 집합의 대표자(부모)를 정해 집합의 노드들이 그 대표자를 가르치고 있다. 이렇게 되면 5번의 부모는 1, 2번의 부모는 1 과 같고 이를 통해 같은 집합에 있다는 것을 알게 된다. 또한 부모의 번호 1, 3, 7을 통해 3개의 집합이 존재한다는 것을 알 수 있다.

재웅쌤의 말을 빌려 다시 설명하자면, 1반과 2반과 3반이 있다. 각 반에는 반의 반장이 존재한다. 1반의 반장은 a, 2반의 반장은 b, 3반의 반장은 c라고 한다. 이때 아무 학생이나 잡고 너 반장 누구야? 했을때 a라고 한 학생과 b 한 학생은 서로 다른 반이라는 것을 알 수 있고 a라고 한 학생과 a라고 한 다른 학생은 같은 반이라는 것을 알 수 있다. 이처럼 유니온 파인드는 대표자를 정해 노드들이 같은 집합인지 판단할때 용이하게 사용된다.

코드를 이용하여 살펴보자.

int parent[] = new int[N] // 노드가 N 개 존재한다.

for (int i = 0; i < n; i++) {
	parent[i] = i;
}

우선 모든 노드들의 대표자는 자기 자신으로 초기화를 한다.

for(int i = 0; i < M; i ++){ //노드 연결 정보가 M 개 존재한다.
	int start = Integer.parseInt(st.nextToken());
	int end = Integer.parseInt(st.nextToken());
    start = findSet(start);
    end = findSet(end);
    if(start!= end){
        unionSet(start, end);
    }
}

다음과 같이 노드 연결 정보를 입력 받는다. findSet 은 해당 노드의 대표자(부모)가 누구인지 찾는 것이다.

그리고 입력받은 두 정보의 대표자를 찾았을 때 만약 대표자가 다르다면 unionSet을 통해 같은 대표자를 가르치도록 해준다.

private static void unionSet(int start, int end) {
	start = findSet(start);
	end = findSet(end);
	if (start != end)
		parent[end] = start;
}

unionSet 은 비교적 간단하다. 대표자를 찾고 대표자가 다르면 뒤에 입력받은 노드의 대표자를 앞에 입력받은 노드의 대표자로 바꾸어 준다.

private static int findSet(int start) {
	if (parent[start] == start)
		return start;
	else {
		int p = findSet(parent[start]);
		parent[start] = p;
		for(int i = 0; i <parent.length ; i++)
		{
			if(parent[i] == start)
				parent[i] = p;
		}
		return p;
	}
}

findSet 은 재귀함수이다. 찾는 노드의 대표자가 자기 자신이면 그 값을 리턴해준다. 만약에 다르다면 재귀를 통해 찾는 노드의 대표자의 대표자를 찾아 찾는 노드의 대표로 지정해준다. 그 후 만약 나를 대표자로 보고 있는 노드가 있다면 그 노드의 대표자 또한 방금 찾은 새로운 대표자로 업데이트를 해준다.

if(parent[0] != parent[1])

이 코드를 통해 대표자의 다르면 다른 무리인 것을 알 수 있다.

int count = 0;
for(int i = 0; i < N; i ++)
{
	if(parent[i] == i)count++;
}

이 코드를 통해 대표자가 자기 자신이면 카운트를 증가시켜 무리의 개수를 셀 수 있다.

최소 스패닝 트리 (Minimum Spanning Tree, MST)

span : 두 곳을 걸친다. 즉 ST 는 모든 노드를 걸치는 나무 , 모든 노드를 연결하는 나무라는 뜻이다.

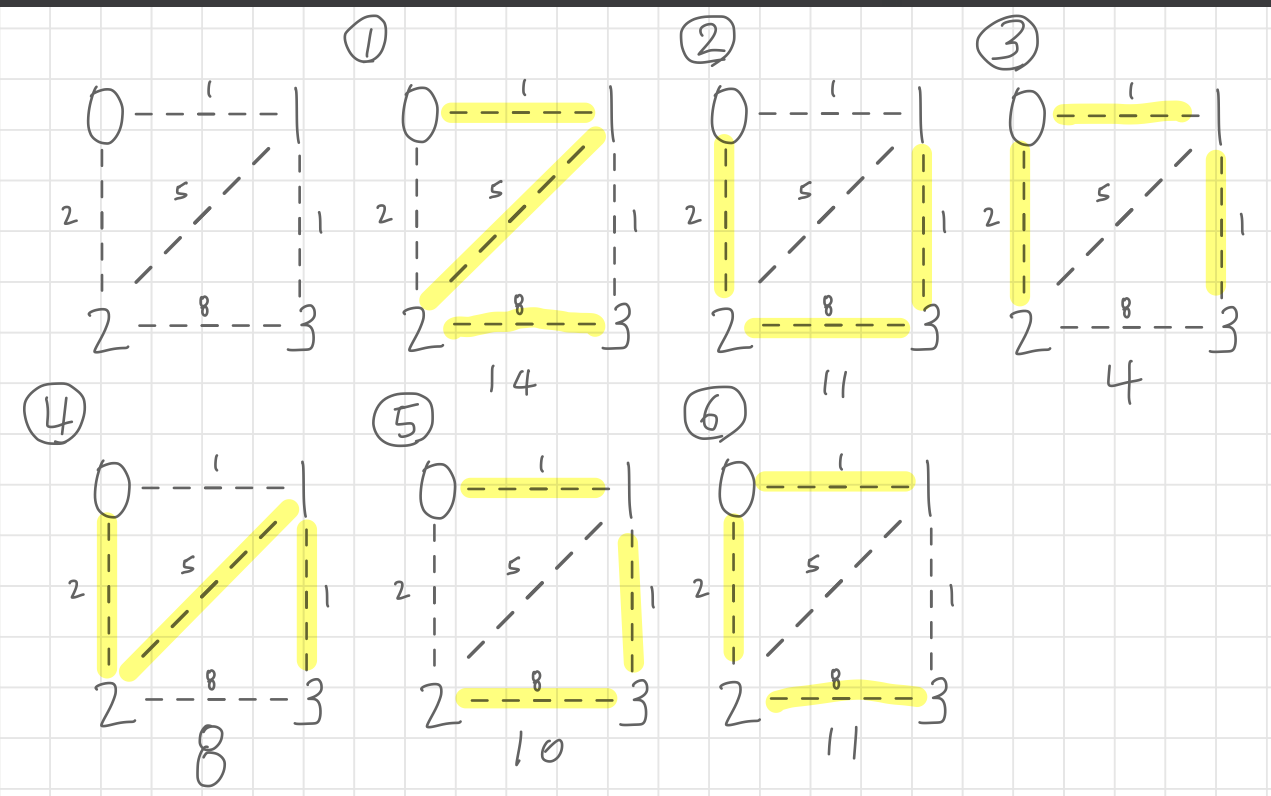
섬 연결하기

그림과 같은 그래프가 있을 때 이 그래프에서 Spanning Tree 는 다음과 같이 여러가지가 존재한다. 최소 스패닝 트리란 모든 노드를 연결한 나무에서 그 가중치의 값이 가장 최소인 그래프를 최소 스패닝 트리라고 한다. 해당 예제에서는 3번의 가중치가 4이므로 3번이 최소 스패닝 트리이다.

크루스칼 알고리즘

크루스칼 알고리즘은 여러 스패닝 트리 중 최소 스패닝 트리를 찾는 알고리즘 이다. 크루스칼 알고리즘은 간선을 작은 순으로 하나씩 탐색하며, 사이클이 생기지 않을 시, 최소 신장트리에 추가하는 그리디 알고리즘이다.

  1. 각 노드들의 연결 정보(간선)와 비용을 저장한다.
  2. 저장된 정보를 비용에 따라 오름차순으로 정렬한다.
  3. 순서대로 간선을 그려보며 싸이클이 생기지 않을 때 그래프에 추가한다.

그래프에 싸이클이 생긴다는 것은 최소 신장 트리가 될 수 없다는 의미이기 때문에 간선을 추가할 때 싸이클이 생기지 않는지 검사를 해야한다. 간선의 양끝 노드들이 같은 집합이면 간선을 추가할 때 사이클이 형성된다는 것을 알 수 있으므로 유니온 파인드를 이용하여 검사가 이루어진다.

[프로그래머스]42861 - 섬 연결하기

위에서 설명한 크루스칼 알고리즘을 이용한다면 쉽게 풀 수 있는 문제이다.

출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges

Tags
comments powered by Disqus